QUANTUM ESPRESSO建模

QUANTUM ESPRESSO的建模教程

转载至：第一性原理计算建模教程

晶体结构要点

首先，说明以下几个概念：平移群，点群，空间群，原胞，晶胞，布拉伐格子，晶系，晶面，布里渊区。

晶体（crystal），是原子、离子或分子周期性排列的结构。

格子（格点）（lattice），是数学上的点构成的周期性结构。

群，是一种代数结构，在集合上封闭的运算，运算满足结合律，存在单位元，存在逆元，定义为群。可以将空间中的晶体格子坐标看成集合，在考虑块材性质时，可以认为晶体在空间无限延伸，允许其转动、平移，则可以构成群，转动、反演为群的运算，或称之为变换、操作。

如果只允许平移，称为平移群。

如果只允许转动（含空间反演、镜像），称为点群，3维空间中的点群有32种。

如果允许转动和平移的复合操作，称为空间群，3维空间中的空间群有230种。指定了空间群的类型，我们只需要知道在空间群操作下不重复的原子位置，就可以确定晶体结构，这些不重复的位置称为Wyckoff位置，QE输入有space_group和ATOMIC_POSITIONS { crystal_sg }来专门设置。

保持平移对称性的最小单元是原胞。

保持平移对称性和点群对称性的最小单元是晶胞。

布拉伐格子是按照基元+格子的概念定义的，确定布拉伐格子应满足：（1）所选平行六面体必须充分反映出格子的点群与平移群，即平行六面体必须与整个格子的晶系特征一致。（2）所选择平行六面体各个棱之间夹角为直角的数目最多，不为直角者尽可能地接近直角。（3）在满足上述（1）（2）条件后，所选择的平行六面体的体积应为最小。布拉伐格子即为晶胞。3维空间的布拉伐格子有14种。下图是14种布拉伐格子的基矢a,b,c及夹角 $\alpha, \beta, \gamma$ 所具有的特定关系。

在特定的平移、旋转操作下，晶体保持不变，这种在某种操作下不变的性质称之为体系的对称性，不同的操作定义了不同的对称性，例如，沿$\vec a$方向平移2个平移基矢等。体系的薛定谔方程，由于体系的对称性，也具有变换下不变的性质，于是有量子数来标记这些变换，晶体平移对称性是一系列准连续的k值所标记的，k点所在空间称为k空间，k空间是相对晶体的原胞定义的，计算晶体的能带就是在k空间进行的，k空间也具有周期性，取原点周围的魏格纳-塞茨原胞，称为第一布里渊区。

晶面是相对于晶胞定义的。

按照晶体具有的点群分类，分为7种晶系（crystal system），即：triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal和cubic。

14种布拉伐格子，分为7种格点系（lattice systems），即：triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal和cubic。

晶系和格点系的区别见注2。

QE中的结构定义

QE输入文件的总体结构如下图，输入文件的前半部分满足Fortran语言的Namelist语法。与结构有关的包括SYSTEM部分的ibrav,celldm,nat,ntyp以及ATOMIC_POSITIONS和CELL_PARAMETERS共三个部分。

QE计算的结构都是在三维空间中周期性重复的，所以需要定义周期性的单元（这里称作CELL，单元）,以及周期性单元内的原子坐标。在QE中用三个矢量$\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}$定义CELL。CELL的定义本身不依赖于空间直角坐标系（笛卡尔坐标系）的选择，只需要定义三个基矢量的长度和三个夹角，但是为了计算，需要确定一个空间直角坐标系，以写出各个矢量的笛卡尔坐标，

这里空间直角坐标系的选取，对于ibrav$\neq$ 0是在QE程序内部进行的，用户不需要设置；对于ibrav=0是用户通过写出CELL_PARAMETERS而确定的。

设置ibrav=0，这时需要在输入文件中写入CELL_PARAMETERS，即CELL的基矢量$\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}$，基矢量是空间直角坐标系中的直角坐标（笛卡尔坐标），空间直角坐标系的选法有一定的任意性，用户可以根据习惯选择，比如，将原点放在某个原子上，将z轴定义为布拉伐格子的基矢c方向，这里坐标系的不同选择，对应的原子坐标会有一个单位正交矩阵所定义的变换，但是建议是右手系。坐标的单位有三种选择：alat，bohr，angstrom，其中，alat是由celldm(1)或A定义的晶格常数单位。设置ibrav=0并写出CELL_PARAMETERS这种方法适合用来设置超胞、slab模型等，也可以用来建原胞，是一种通用性较好的方法，并且与其他结构文件（cif，VESTA，POSCAR等）格式转换较为方便，也更方便进行后续计算。

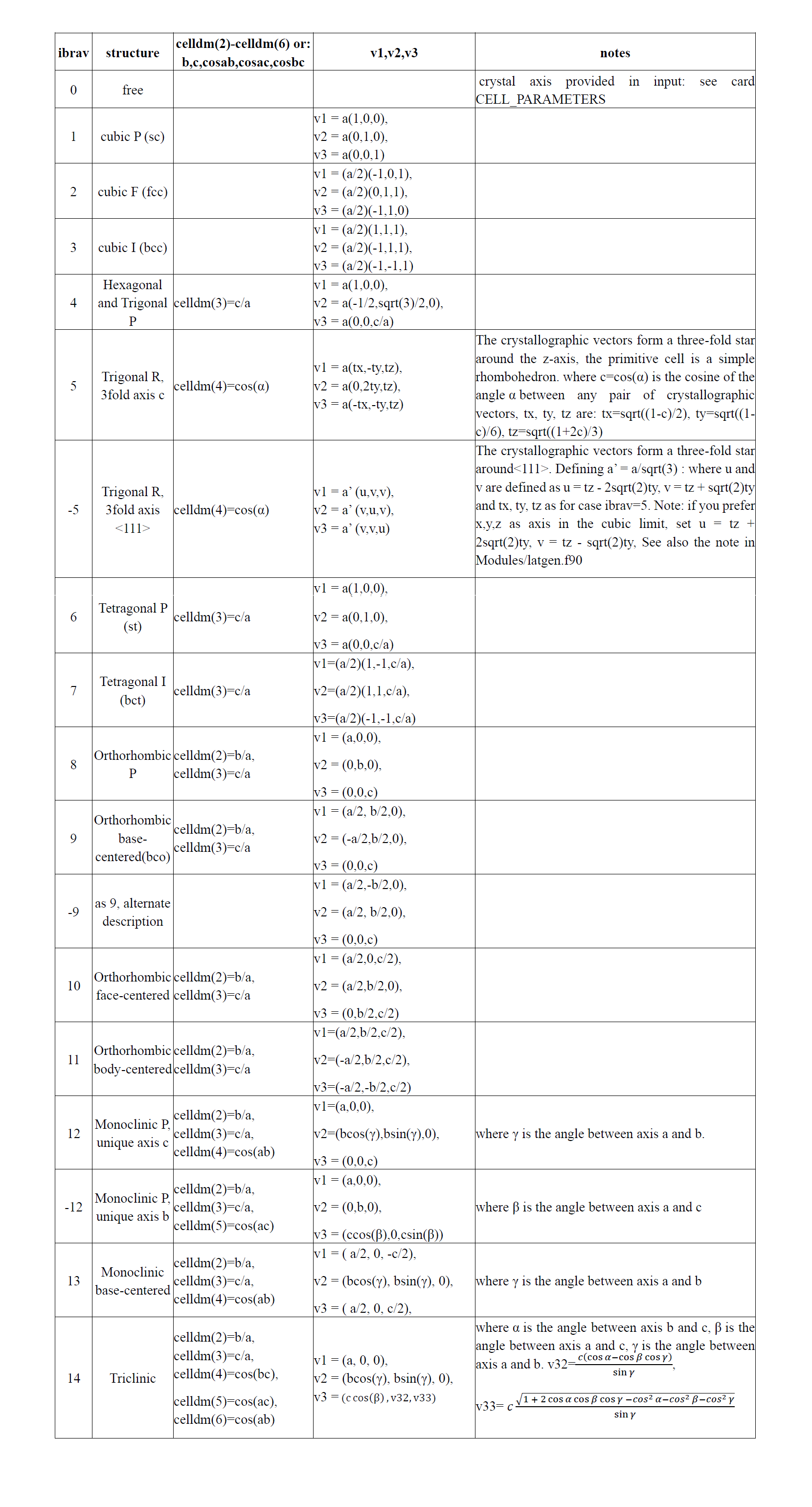
设置ibrav$\neq$ 0，这时会生成布拉伐格子相应的原胞。表1列出了ibrav和celldm设置以及对应的$\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}$原胞基矢量（相当于内部生成的CELL_PARAMETERS），注意celldm(1)定义了alat，单位只能是Bohr；celldm(2)和celldm(3)定义的是比例b/a和c/a，而不是基矢长度，celldm(4:6)是角度的余弦值，角度通常是布拉伐格子晶胞的基矢量夹角；对于ibrav=-3,-5,-9,91,-12,-13分别不同的空间直角坐标系的取法，或不同的原胞基矢量取法；ibrav$\neq$ 0中的简单格子也可以用来设置超胞等结构（对于超胞不要再使用面心、体心等非简单格子）。注1 注2

在QE中还可以直接给出晶格的基矢长度和夹角A, B, C, cosAB, cosAC, cosBC，单位是Angstrom，和celldm一样，唯一地确定了CELL，定义了$\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}$，这时的空间直角坐标系是QE内部定义的，也由表1（基于qe-6.0，请对照具体使用的版本，可能有出入）给出。

在定义了CELL之后，用ATOMIC_POSITIONS定义CELL中原子的坐标。ATOMIC_POSITIONS的单位有以下可供选择{ alat | bohr | angstrom | crystal | crystal_sg }，其中，crystal是指以$\vec{v_{1}},\vec{v_{2}},\vec{v_{3}}$为基矢量的分数坐标，$\vec{X}=(x_{1},x_{2},x_{3})^{T}=x_{1}\vec{v_{1}}+x_{2}\vec{v_{2}}+x_{3}\vec{v_{3}}$。如果选择{ alat | bohr | angstrom}，则原子坐标是空间直角坐标，由于结构的周期性，这里的空间直角坐标系的选择是任意的，但是习惯上还是与CELL的空间直角坐标系保持一致，坐标值在CELL_PARAMTERS所定义的平行六面体内部。{crystal_sg}是在指定了空间群之后，定义对称性不等价的原子位置，与space_group, uniqueb, origin_choice, rhombohedral配套使用。

QE提供多种方式完成一件任务的设计风格，为具有各种习惯的用户提供了得心应手的工具，但是对于初学者来说，难免有一种眼花缭乱的感觉，这里推荐的方法：

(1)设置ibrav$\neq$0，对于原胞用相应的ibrav类型，对于超胞用简单格子的ibrav，写出celldm(1-6)，这时不写CELL_PARAMETERS，输出会内部生成CELL_PARAMETERS以alat（celldm(1)）为单位。VESTA画图时用输出里的CELL_PARAMETERS，需要转换单位。转为POSCAR格式可以用densityflow.com的工具。

(2)设置ibrav=0，写出以Angstrom为单位的CELL_PARAMETERS (angstrom)，对于原子坐标建议使用分数坐标，即写成ATOMIC_POSITIONS (crystal)，不设置celldm(1)，这时，alat和celldm(1)由程序内部设置成v1的长度，以Bohr为单位（1 Bohr = 0.52917720859 Angstrom）。VESTA画图CELL_PARAMETERS已经是Å为单位。

第二种设置ibrav=0后续处理时要注意pp.x输出电荷等文件是以alat为单位输出CELL_PARAMETERS的，而与输入文件的单位不一样。vc-relax计算的最终结构是以ibrav=0搭配CELL_PARAMETERS (angstrom)的格式输出的。要注意基矢和原子坐标的有效数字位数要写得多一些，以找到正确的对称性。ibrav=0一个不足之处是输出了点群操作但是没有输出点群名称（需设置verbosity='high'），可以将qe_release_6.4/ PW/src/summary.f90第608行IF ( ibrav == 0 ) RETURN加注释，重新编译。

最后，强烈建议做好结构之后，用可视化的软件如VESTA、Xcrysden、MS等画出晶体结构，检查一下原子间距、键角等是否正确，这些软件并不都支持QE的输入格式，可能需要转换格式，这时用ibrav=0也比较有利。用VESTA画图，转为POSCAR格式，输入文件拷贝CELL_PARAMETERS后面的三行作为POSCAR的第3-5行（POSCAR第二行设置为1.0），拷贝ATOMIC_POSITIONS (crystal)后面的坐标后三列，作为POSCAR里的Direct坐标，QE输出转POSCAR同上。

QE结构设置的种类总结如下，除了通过空间群设置以外，单元有6种设置方法，原子坐标有4种设置方法，一共有24种组合方式，当然，每一种都是等价的，从任意一种可以推出其余的23种，转换工具见densityflow.com。考虑到ibrav=0时存在直角坐标系选取的任意性，ibrav=0、CELL_PARAMETERS( alat )、celldm(1)设置存在alat选取的任意性，这种转换有可能是不可逆的。对于一种ibrav设置，只是对应布拉伐格子类型的一种单元设置，比如体心立方就有ibrav=3和-3两种单元设置，所以通过CELL_PARAMETERS进行单元设置，在进行上述转换时，可能会转到不同的布拉伐格子，比如将体心立方的某种单元设置（不能归为3或-3）转为其他的ibrav类型。

注：自6.4.1版本，官方不推荐celldm(1)=1.88972613（任何<2的值）的做法，这里也修正为celldm(1)设置为晶格常数，或用ibrav$\neq$ 0。

注2：关于alat，alat是qe内部定义的量，以Bohr为单位，具有晶格常数的意义，在pw.x的输出接近开头处有 lattice parameter (alat) = x.xxxx a.u.。(1)当ibrav=0，且CELL_PARAMETER{bohr或angstrom}时，alat是CELL_PARAMETER第一行矢量的长度，此时不允许写celldm，否则会和CELL_PARAMETER冲突；(2)当ibrav=0，且CELL_PARAMETER{alat}时， alat=celldm(1)或A，这里celldm(1)或A取值有一定的任意性，这里建议取为第一个基矢量的长度，即具有晶格常数的意义；(3)对于ibrav$\neq$0，alat=celldm(1)或A。对于输入，alat可能的影响是使用CELL_PARAMETER {alat}，这时cell参数是以alat为单位的。对于输出，pw.x有些输出量用到了alat为单位，这里就不再列举，根据情况判断。

晶胞和原胞的相互转换

原胞是保持平移对称性的最小单元，所以，在计算能带、声子色散时，研究对象是原胞（声子的有限位移方法需要超胞，但是，这时的超胞是一个辅助系统，色散仍然是针对原胞画的）。用比原胞更大的单元计算能带会造成band folding现象，即能带折叠，相当于布里渊区变小了，布里渊区的形状也可能发生了变化，从超胞到原胞的能带可以通过band unfolding还原到原胞的能带。

文献通常按照以下约定：晶胞是定义晶面、晶向、超胞的参照，而不是原胞或其他单元。

首先，定义一般的周期性单元CELL的变换。按照文献[1]的约定，将（分数）坐标写为列矢量，基矢量$\vec{a},\vec{b},\vec{c}$ 也各为列矢量。点X在基矢$O,\vec{a},\vec{b},\vec{c}$（$O$为原点）下的坐标$(x_{1},x_{2},x_{3})^{T}$定义为

考虑晶格静止不动，选择不同的基矢，即选取不同的CELL，同一个点X对新的基矢$O’,\vec{a’},\vec{b’},\vec{c’}$有坐标 \(\vec{X'}=(x'_{1},x'_{2},x'_{3})^{T}=x'_{1}\vec{a'}+x'_{2}\vec{b'}+x'_{3}\vec{c'}\) 下面给出有撇号和无撇号的基矢选择下基矢和坐标的变换关系。

周期性单元CELL的变换是一种特殊的仿射变换（数学上一般的仿射变换形成的新单元并不保证具有晶格周期性），可以分解为线性部分和平移两个部分。

线性部分包括基矢方向和长度的改变，由一个矩阵$\mathbf{P}$表示。 \((\vec{a'},\vec{b'},\vec{c'})=(\vec{a},\vec{b},\vec{c})\mathbf{P}=(\vec{a},\vec{b},\vec{c})\quad \begin{pmatrix} P_{11}& P_{12} &P_{13} \\ P_{21}& P_{22} &P_{23} \\ P_{31}& P_{32} &P_{33} \\ \end{pmatrix} \quad\\ =(P_{11}\vec{a}+P_{21}\vec{b}+P_{31}\vec{c}, P_{12}\vec{a}+P_{22}\vec{b}+P_{32}\vec{c}, P_{13}\vec{a}+P_{23}\vec{b}+P_{33}\vec{c} )\)

知道了矩阵$\mathbf{P}$和逆矩阵$\mathbf{Q}=\mathbf{P}^{-1}$，就可以进行CELL之间的变换，常见的晶胞转换为原胞的变换矩阵由表2给出，反之交换$\mathbf{P}$和$\mathbf{Q}$得到。注意这里的矩阵选取并不是唯一的，这里选择的原胞基矢的原点和晶胞基矢的原点是重合的，即没有平移。

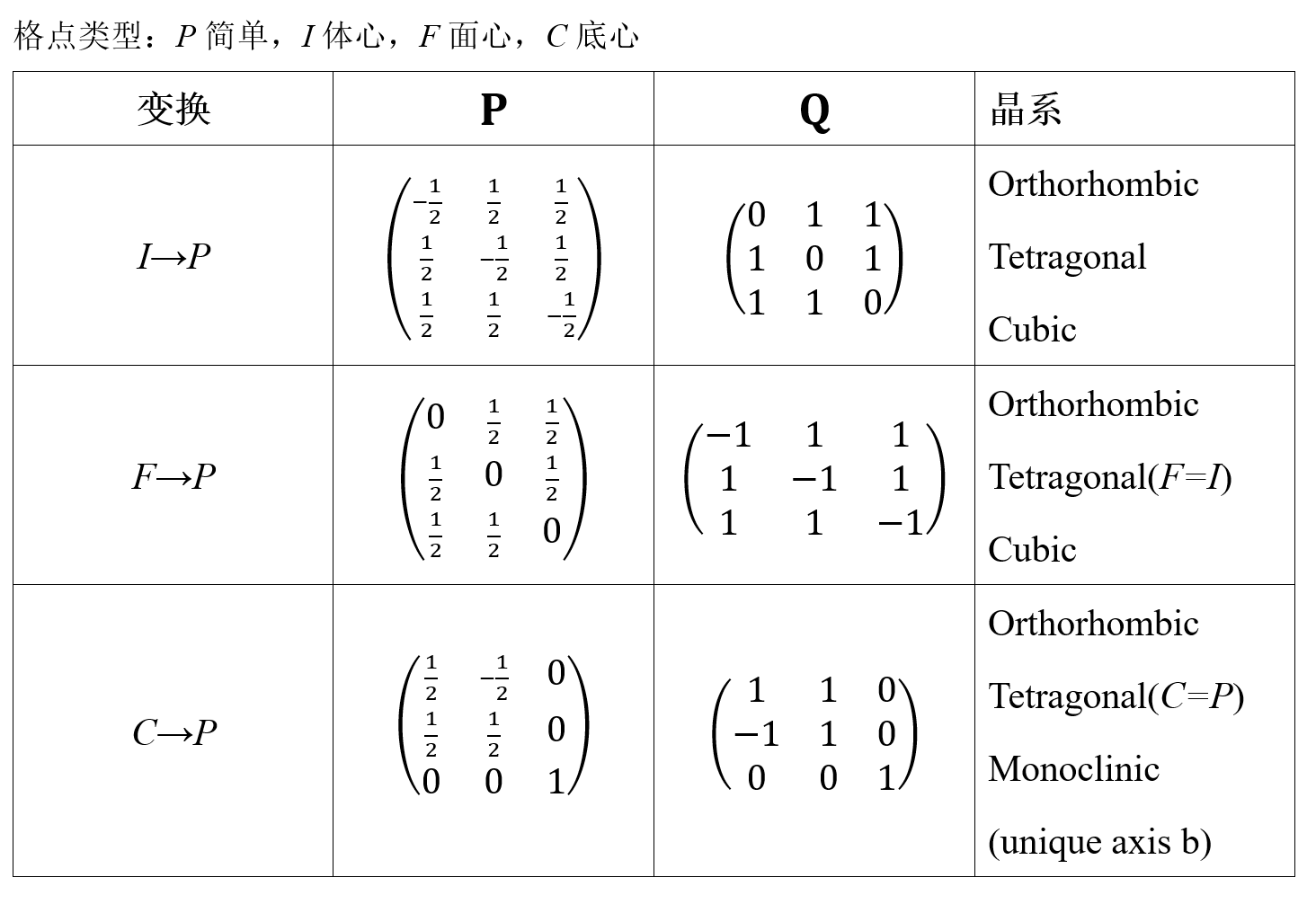
对于菱方布拉伐格子，见注2的7种空间群，cif生成的是六方的晶胞，体积是菱方的3倍，原胞计算用（ibrav=5，同时定义celldm(1)和celldm(4)），用ibrav=0时也存着晶胞转原胞的问题，转换矩阵如下，参见注1 ： \(H \rightarrow R \\ P=\quad \begin{pmatrix} 2\over 3 & -{1 \over 3} & -{1 \over 3} \\ 1 \over 3 & 1 \over 3 & -{2 \over 3} \\ 1 \over 3 & 1 \over 3 & 1 \over 3 \\ \end{pmatrix} \quad Q=\quad \begin{pmatrix} 1 & 0 & 1 \\ -1 & 1 & 1 \\ 0 &-1 & 1 \\ \end{pmatrix}\)

周期性单元CELL的变换，还可以包含平移，平移$\vec{p}$用变换前的基矢定义为：$\vec{p}=p_{1}\vec{a}+p_{2}\vec{b}+p_{3}\vec{c}$。平移的逆变换$\vec{q}=q_{1}\vec{a’}+q_{2}\vec{b’}+q_{3}\vec{c’}$，有$\vec{q}=-\mathbf{P}^{-1}\vec{p}$。

分数坐标的变换公式为： \(\quad \begin{pmatrix} x^\prime_{1} \\ x^\prime_{2} \\ x^\prime_{3} \end{pmatrix} \quad=\mathbf{Q} \quad \begin{pmatrix} x_{1} \\ x_{2} \\ x_{3} \end{pmatrix} \quad+\vec{q}\)

将晶胞转换为原胞，因为晶胞和原胞中的原子个数不同，坐标变换后会有重复或相差一个原胞格子，需要将重复的删去。反之，将原胞转换为晶胞，需要将原胞格子重复足够大以覆盖晶胞，重复后的原子分别变换到新的分数坐标，最后保留晶胞内部的原子（分数坐标在0到1之间）。

以底心单斜碳的同素异形体为例[4]，用TransCell变换CELL和原子坐标，并用VESTA验证。

先下载cif文件，用VESTA打开，画出晶胞如下：

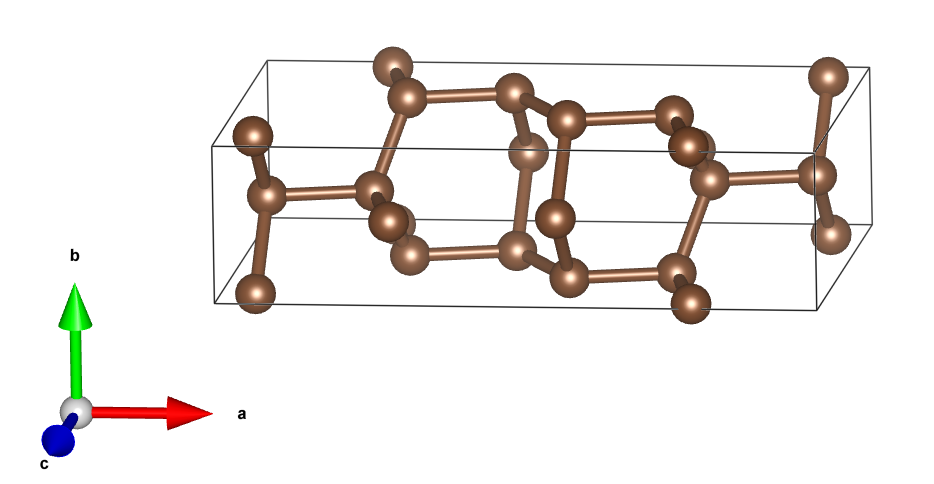
输入转换矩阵：

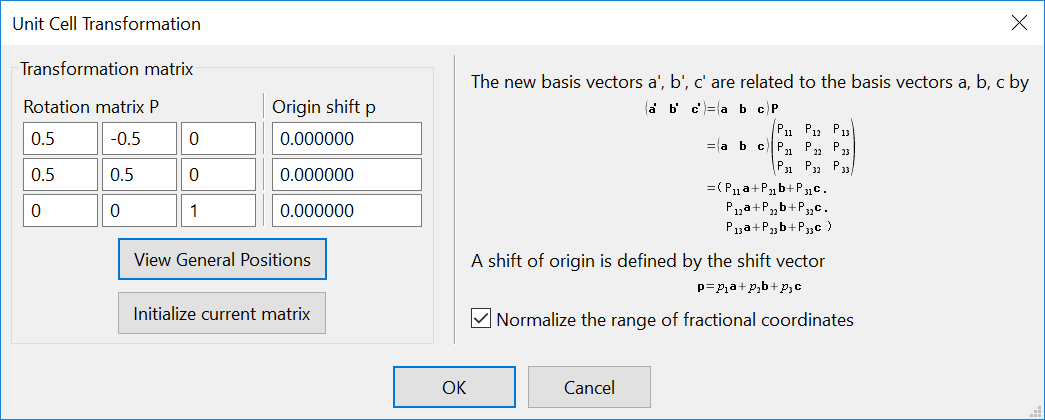
得到原胞：

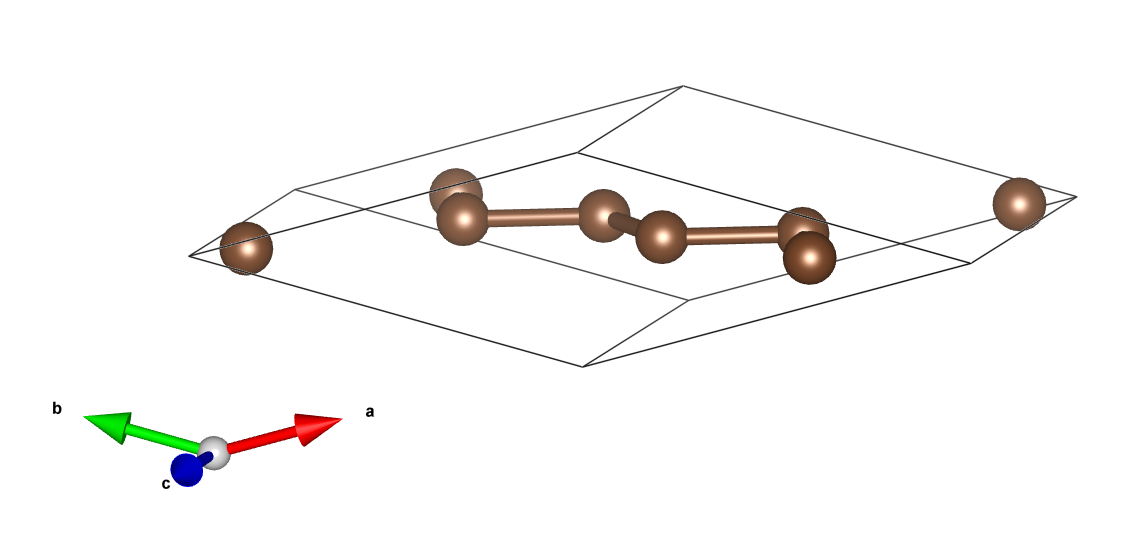
原胞和晶胞的比较（见aflow）：

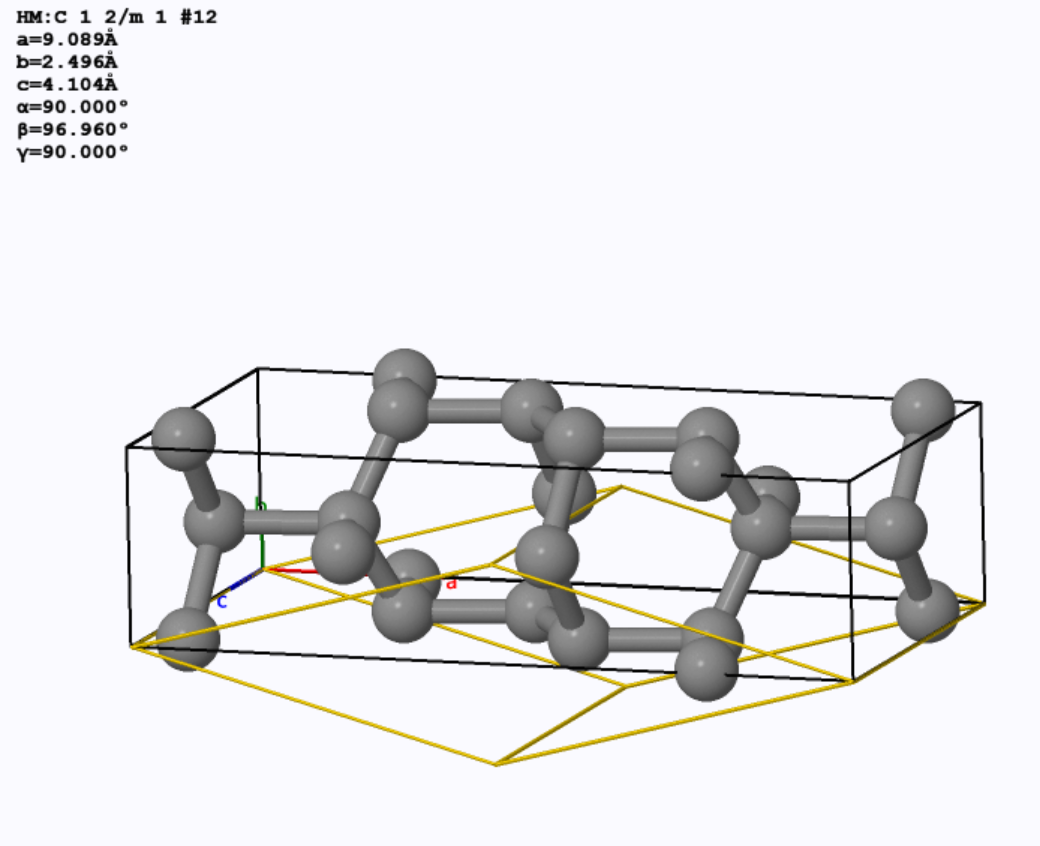
分数坐标和直角坐标的相互转换

上一节的变换矩阵推导中并没有用到晶体周期性，所以可以将直角坐标看成单位正交矢量作为格子的基矢，这时CELL基矢列矢量组成的矩阵即为单位格子到CELL的变换矩阵，而逆矩阵即为倒格子基矢量组成的矩阵(或相差一个常数系数)。

非周期性系统

分子、团簇、纳米晶体、具有点缺陷的固体等不具有周期性，纳米线是1维周期性的，固体表面、量子阱、二维材料等是2维周期性的，QE这样的基于平面波基函数的程序，对于这些非三维周期性的材料需要采取超胞近似，选取足够大的周期单元，并且，需要时在CELL中的一部分空间不加入任何原子，也就是引入真空，以隔离非周期性的维度。

平板（slab）模型的建立

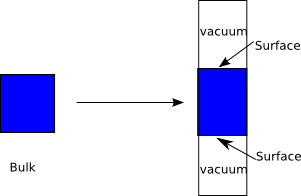
对于固体表面，平面波计算要首先建立平板模型，选取垂直晶面方向足够厚的平板，并且加入足够厚的真空，以消除表面之间的作用，实现表面性质的计算。对于异质结构，如超晶格，需要建立repeated-slab模型，二维材料异质结，如双层石墨烯“魔角”，模型建立也会遇到有共性的问题。

对于有重构（也叫再构，reconstruction，是指表面原子发生面内平移对称性的变化）的晶体表面，要按照重构截取面内的单元，重构原子的坐标要按照实验结构或经验手动设置，这是因为如果初始位置与要研究的重构表面如果相差较大，及时原子个数相同，弛豫的结果也可能是某个亚稳态结构，所以通过relax不能保证弛豫到要研究的特定重构表面结构。

对于没有重构的晶体表面，需要考虑如下：

首先，确定要计算的晶面。晶面用密勒指数标记，密勒指数是不过原点的平面在基矢方向的截距倒数约化成的整数比，注意密勒指数是相对晶胞定义的，通常是三个数，如(001)，(110), (531)等等，一般低密勒指数的面较常见，但实验上也会出现高密勒指数的面。对于六方和三方（菱方）晶体，习惯上用四个数的密勒指数，如(0001),(1$\overline{1}$01)等，这里是选了垂直三重旋转轴的面内3个基矢以及沿着三重旋转轴的1个基矢，一共4个基矢而定义的密勒指数，其中，前三个指数的和一定是零，所以只有3个独立的指数，有的文献对于六方或三方结构的晶面也用三指数的表示。晶面确定后，还要根据实验确定表面原子的种类，实验上由于生长条件不同可能有多种表面原子的情况，例如GaN(0001)的表面有Ga和N原子截止的不同情况。

第二，要找到面内的最小周期性单元。先通过密勒指数的定义找到一个面内周期单元（可能非最小），以这个面内周期单位为基础，找最小单元通常用蛮力法从小到大寻找若干组，对于超胞中每一个原子，分别找到面内的最小的几个单元，在不同原子取法中，找到共同面内周期单元中最小的一个，即是要找的表面结构二维最小单元，这时找到的单元并不唯一，选取$a \le b$，夹角有90度选为90度，六方按照文献常见的取为120度，其余选为最接近90度的锐角。

开源项目SlabMaker，提供了建slab的功能，并且提供了在线QE建模工具http://densityflow.com, http://117.51.145.214。其他的实现，包括用MS的建模模块进行；公开的其他来源的讨论包括文献[5]。

第三，确定平板和真空的厚度。无论在平板内两个表面的距离，还是真空两边表面的距离都要足够大，以隔离两个表面的作用，模拟固体表面的性质，真空至少需要10Å到20Å。建议真空放在CELL的z方向的两端（如上图，垂直表面方向记为z）。有时，为了方便，Slab模型的CELL的基矢并不是正交的，但是考虑到周期性这种CELL与正交是等价的。有的文献描述平板厚度时，提到了层（layer）的概念，层并没有无争议的定义，需要依情况而定。有时，材料在垂直晶面方向有周期性，那么层可能是周期的个数；而另一些材料有若干层原子为一组，组与组之间距离较大可以明显划分开，这里的组就是层；还有的材料，在垂直晶面方向杂乱无章，一个原子或几个具有相同z坐标的原子就是一层。

建好超胞之后，变换CELL原子和分数坐标的方法为：将空间直角坐标系做旋转，总可以实现x轴沿第一个基矢（记为$\vec{a}$）方向，z轴与x轴垂直且沿第三个基矢（记为$\vec{c}$）方向（原第一和第三基矢不垂直的，由于三维周期性，也可以将第三基矢投影到垂直表面方向，从而与第一基矢垂直），首先，将第三基矢投影到垂直表面方向：

$\vec{\tilde{c}}
= (\vec a \times \vec b)\frac {\vec{c} \cdot (\vec a \times \vec b)} {\lvert\vec a \times \vec b\rvert^2} $

再将CELL变换为：

真空厚度记为$d_{vacuum}$，找到原子分数坐标最大和最小的两个原子，新的z方向长度为\(\vert\vec c^{\prime}\vert=(x_{max,3}-x_{min,3})\vert\vec c\vert+d_{vacuum}\)。加入真空后，分数坐标如下变换，可以将真空置于CELL的两端，

下面以$\alpha-Al_{2}O_{3}$的(110)面为例，用SlabMaker建slab模型，并用VESTA画图。

从COD下载$\alpha-Al_{2}O_{3}$的cif文件，用VESTA打开，材料具有菱方的原胞，密勒指数是相对晶胞定义的，画出六方的晶胞如下：

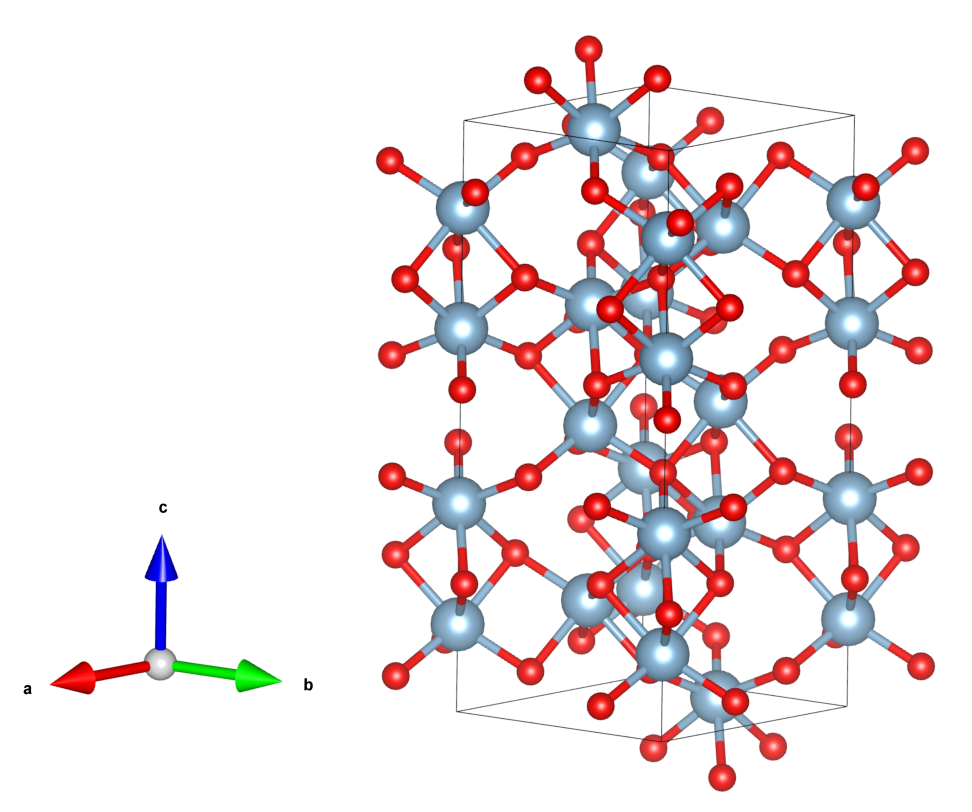
用VESTA导出POSCAR格式文件，命名为Al2O3.vasp。

从这里下载build.py文件，运行python

1
2
3
4
5
    from build import CELL
    unit=CELL("Al2O3.vasp")

    slab=unit.makeslab([1,1,0], layer=2)
    slab.print_poscar("./tmp/slab.vasp")

得到变换矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
P1 =  [[ 1.  0.  2.]
 [-1.  0.  2.]
 [ 0. -1.  0.]]
P2 =  [[-3.33333328e-01  6.66666672e-01  0.00000000e+00]
 [-3.33333313e-01 -3.33333313e-01  0.00000000e+00]
 [ 3.00064645e-09  3.00064645e-09  1.00000000e+00]]
reduced slab cell 
 [[-2.74760979e+00 -4.33033313e+00  7.13849973e-08]
 [ 5.49521970e+00 -4.33033313e+00  7.13849973e-08]
 [ 0.00000000e+00  0.00000000e+00  2.37898727e+01]]
reduced slab No. of atoms:  40
slab and vacuum length:  8.78987274001554 15.0 Ang.
inplane edge and angle:  5.128464149403621 6.99637224468677 84.15650034981714  degree.
reduced slab cell area:  35.694197603259965  Ang^2.

其中变换P1是得到一个预选的cell，对预选cell加入真空，转动c沿着垂直表面方向（变换矩阵见前文），变换P2是将cell约化到具有110面内最小二维周期单元的slab，面内基矢量的夹角是84.16°，结果参考见[6]。

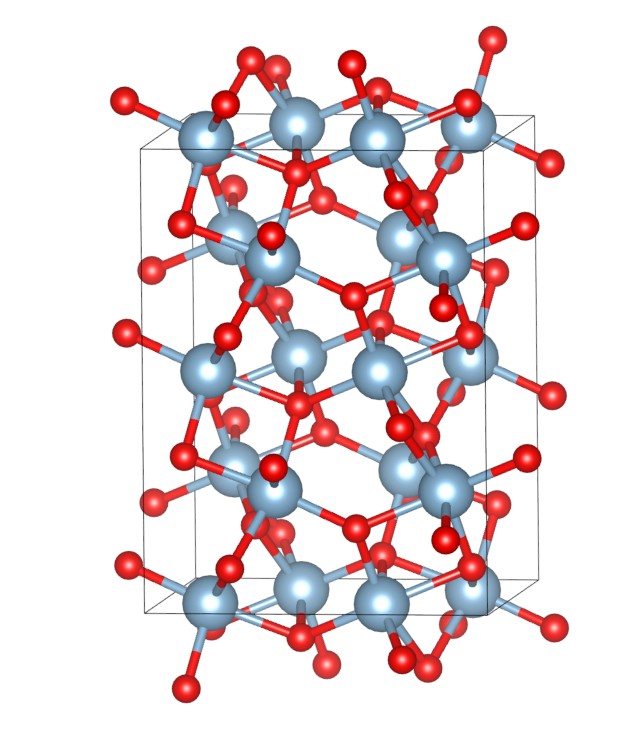
build.py输出了slab的POSCAR（真空厚度和层数在源程序中设置），见运行目录的tmp/slab.vasp。最终slab如图。

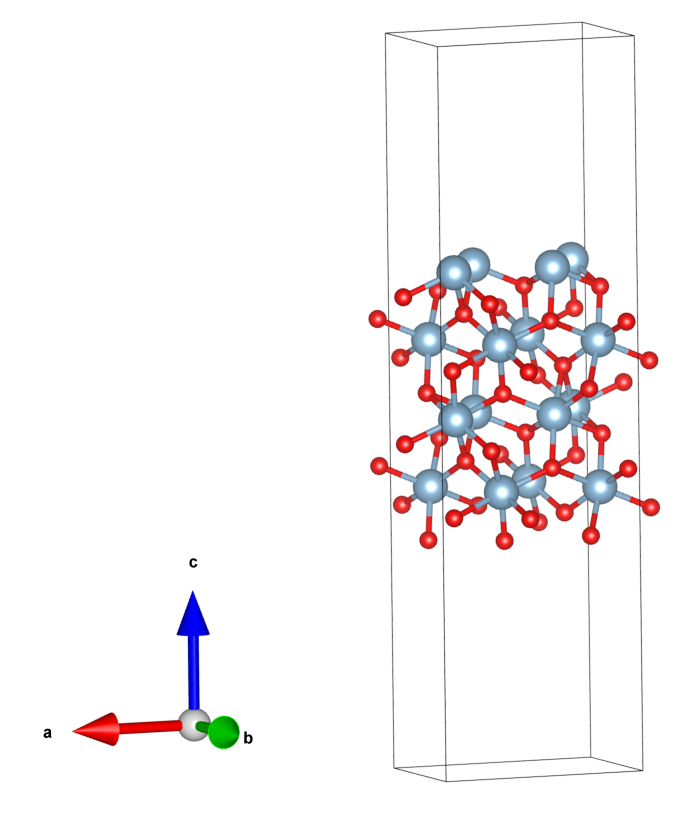
以上是slab的c方向恰好具有周期性的情况，另外一种则当cell的c方向沿着表面法向时，表面法向不具有周期性（或具有极长的周期性），不同于文献[5]的做法，这里在加入真空之后，将cell的c投影到z方向，由于面内的周期性边界条件，这么做是可行的。下面以$\alpha-Al_{2}O_{3}$的(104)面为例（这与文献[5]的$\alpha-Fe_{2}O_{3}$是同一种结构）。

1
2
3
4
5
6
from build import CELL

unit=CELL("Al2O3.vasp")

slab=unit.makeslab([1,0,4], layer=1)
slab.print_poscar("./slab.vasp")

得到slab.vasp，用VESTA画图如下。

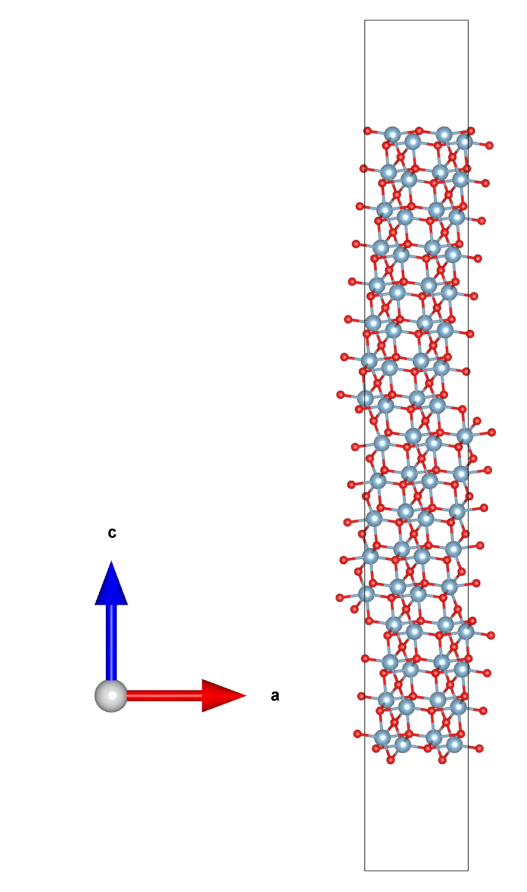
可以看到与文献[5]Fig.1(d)的面内是等价的，cell的c沿垂直表面方向有利于如功函数等的计算。建好slab之后，可以根据需要删掉部分原子以得到特定的截止表面和厚度。

注释

1. 注意晶胞和原胞的区别，对于非简单格子ibrav$\neq0$适合于设置原胞（对于简单格子ibrav$\neq$0当然也是设置了原胞），布拉伐格子中的7个简单格子本身就是原胞，而且，除了菱方外的6个简单格子，不仅是原胞，同时也是晶胞，菱方的布拉伐格子是原胞但不是晶胞，菱方的晶胞是六方的简单格子，体积是原胞的3倍，而底心、面心、体心的7个布拉伐格子本身是晶胞，存在体积更小的原胞。

2. trigonal三方晶系有两种布拉伐格子，一种是ibrav=5，菱方（rhombohedral）布拉伐格子，另一种是ibrav=4，六方（hexgonal）布拉伐格子，晶体属于菱方还是六方要看具体的空间群，在hexgonal和trigonal晶系中，7个空间群（$R3, R\overline{3}, R32, R3m, R3c, R\overline{3}m, R\overline{3}c$）具有菱方布拉伐格子的原胞，其余的45个空间群具有六方布拉伐格子的原胞。这里的菱方和六方是指晶体的格点系统lattice system，而非晶系，格点系统是按照布拉伐格子分类的，晶系是按照晶体点群分类的。

References

1. International Tables for Crystallography (2006). Vol. A, Chapter 5.1, pp. 78–85.

2. https://en.wikipedia.org/wiki/Bravais_lattice

3. http://www.quantum-espresso.org/Doc/INPUT_PW.html

4. Q. Li et. al., Superhard Monoclinic Polymorph of Carbon, Phys. Rev. Lett. 102, 175506 (2009), doi:10.1103/PhysRevLett.102.175506.A. R. Oganov and C. W. Glass, Crystal structure prediction using em ab initio evolutionary techniques: Principles and applications, J. Chem. Phys. 124, 244704 (2006), doi:10.1063/1.2210932.

5. Wenhao Sun, Gerbrand Ceder, Efficient creation and convergence of surface slabs. Surface Science 617 (2013) 53–59.

6. Takahiro Kurita, Kazuyuki Uchida, and Atsushi Oshiyama, Atomic and electronic structures of α-Al2O3 surfaces, Phys. Rev. B 82, 155319(2010).

• Previous
  QUANTUM ESPRESSO v6.8安装
• Next
  QUANTUM ESPRESSO：dos